割り算から動算へ
誰でもわかる大和算解説vol.2
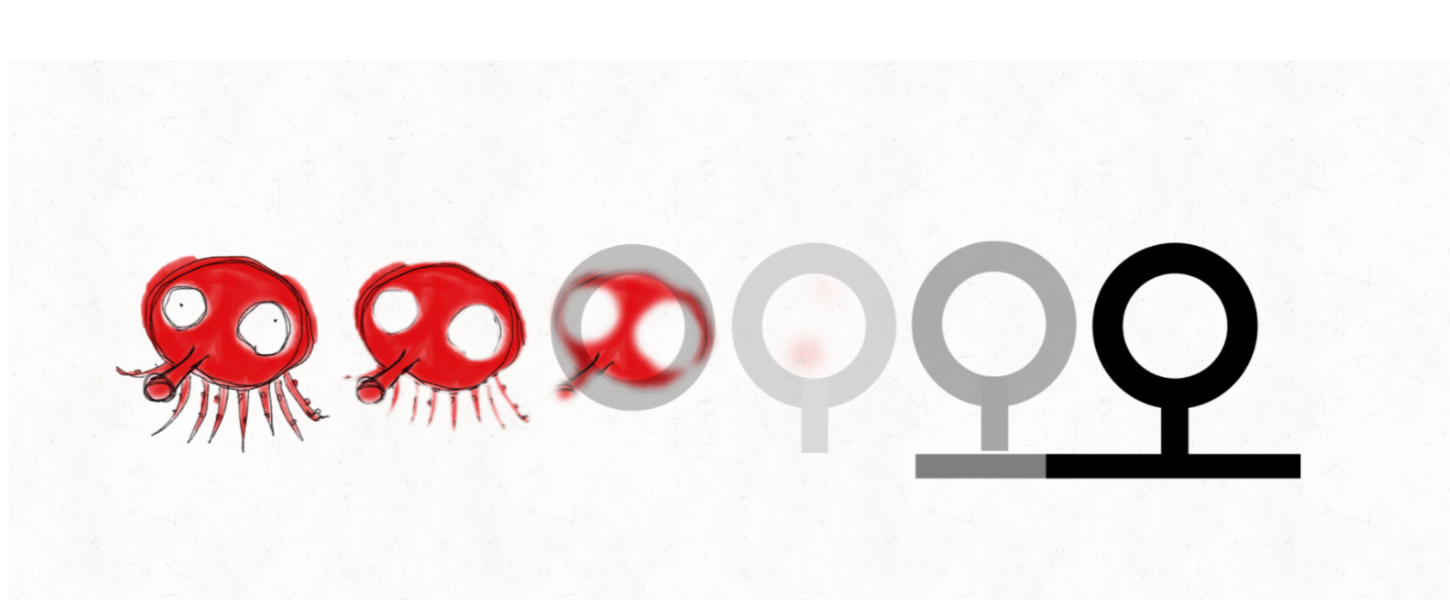
割り算の矛盾を突きつめたら、宇宙全ての創造の原理が解けちゃった!
新しい数理「四則和算」を、子どもから大人まで理解できるよう、簡単なアニメーションにしました。
目次
大人の常識ぶっ壊す!シン数理vol.2〜割り算の矛盾から動算へ
vol.1がまだの方はこちらからご覧ください。
まずは、動画vol.2をご覧ください。
割り算から切り算、切り算から動算へ
さて、vol.1では、現実をありのまま表現できない「割り算」の矛盾点の1つ。
等分にすると、1つの断片が残りますが、残りが消えてしまうことを指摘しました。
その代わりになる切り算では、
1cut2=1/2+1/2 もしくは、1cut2=0.5+0.5
と表現しました。
が、現実的には、ぴったり半分に切れることはありません。
そこで登場するのが、「+」の代わりになるこの記号
「오 」
これは、自由に動くレバーです。
1つのものを、自由な数・自由な量に切り分けることができます。
数と量を同時に計算できるというのが、動算のポイントです。
数と量〜デジタルとアナログの違いを明確に
ここで、押さえておきたいのが、数と量。
デジタルとアナログの違いです。
一般には、「コンピューターの世界は、デジタル」「自然は、アナログ」「デジタルは新しくて、アナログは古くさい」などというイメージがあるかも知れません。
でも、現実はデジタルとアナログの両方の要素があります。
デジタルとは、1つ、2つと数えられる分離した数。
アナログとは、測ることができる連続した量。
そして、デジタルとアナログを同時に現すのが「Quantal(クオンタル)」です。
クオンタルとは、東京大学・道徳感情数理工学研究室の光吉俊二特任特任准教授が提唱する、デジタルの次世代概念です。
※「An Artificial Ego Architecture〜人工自我の基本設計」DHU JOURNAL Vol.07 2020 東京大学大学院工学系研究科 特任准教授 光吉 俊二ら
既存の機械学習やAIなどに用いられているのは、0と1の二進法を使ったデジタルのみです。
でも、当然ながら、人の心や情緒は、デジタルのような二元論ではなく、どこまでも連続したアナログの要素もあります。
ありのままの世界を表現したり、人の良きパートナーとなる人工自我を実現するには、クオンタルへのバージョンアップが必須となるでしょう。
ここで、デジタルとアナログの違いを理解し、明確にしておくことで、後々、クオンタルへの理解が深まります。
大和算によって導き出される最終定理の理解のためにも、いま、ここを押さえておくことが重要です。
算数が苦手であった筆者も、vol.2のアニメを作る過程で、この違いがよく分かっていなかったために、算数がちんぷんかんぷんだったのだということがよく理解できました。
光吉俊二特任准教授は、小学生の頃から、この割り算の矛盾や不便さに違和感を抱いており、それを突き詰めることでこの新しい数理を発明するに至ったそうです。
数(分離数):デジタルとは?
人が、これとそれは別々の存在だと認識しているものを、1つ2つと数える際に使うのが、「数(分離数)」です。
1つの存在は、1より小さくは分割できず、1より小さい値は、0(ゼロ)になります。
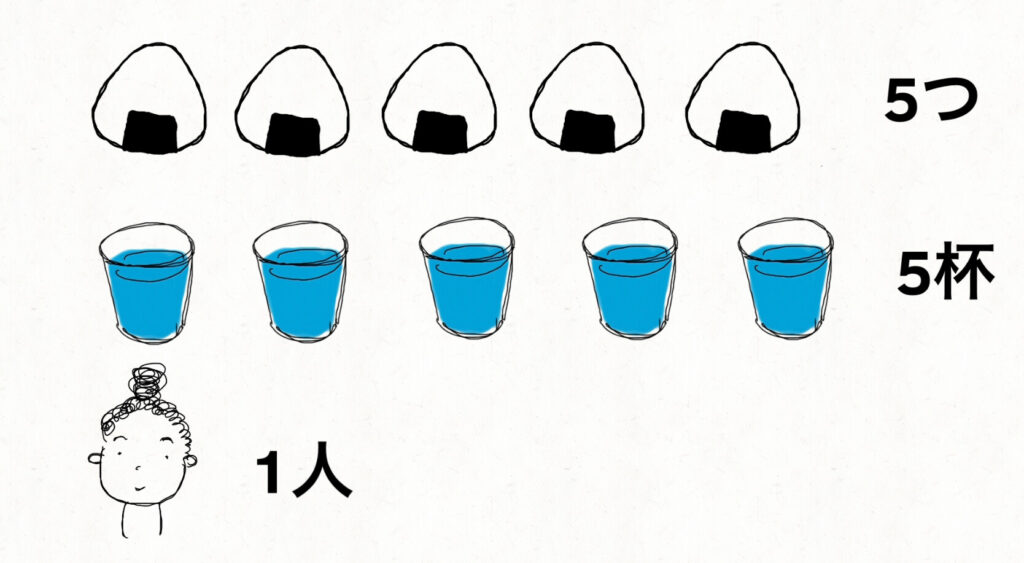
例えば、コップに入った水はバラバラの存在なので、1杯、2杯と数えられます。
現在のコンピューターは、二進法による0と1のみのデジタルで計算しています。
0と1の間にある連続性は表現することができません。
量(連続量):アナログとは?
連続量は、その存在の長さや体積、重さなどを測るときに用います。
さらには、面積、密度、時間、力、速度なども連続量とされます。
1以下、無限に小さくすることができます(無限小)。
例えば、コップに入った水は、1杯という分離数で数えられますが、その中にある水は、連続している量として、測ることができます。
普段、私たちは、分離数と連続量をあまり区別していないのではないでしょうか?
例えば、1年の内には、連続的な時間が流れています。
でも、カレンダー上は、1月から12月まで、12個のバラバラの月に分けられます。
そんな風に、私たちは、本質的には連続しているものを、バラバラに分け、この世界を分かりやすく認識しています。
割算と切算・動算の比較
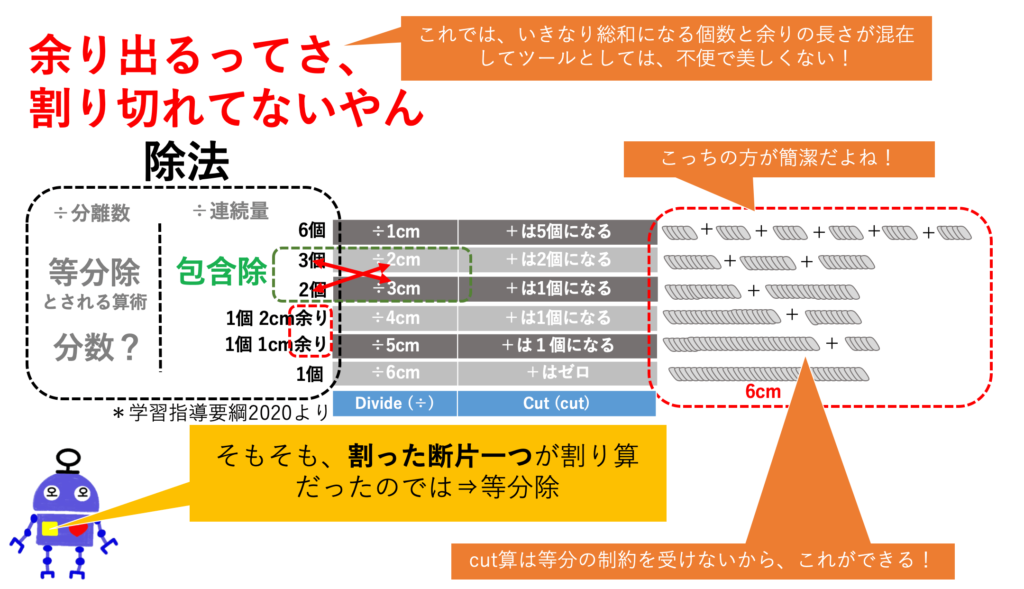
ここで、割り算(除法)と切り算・動算を比較してみましょう。
上のスライドは、6cmの縄を切り分ける場合です。
スライドの左側が、割り算、右側が切り算を使った場合です。
(切り算の「+」を、自由に切り分ける「오」にしたものが、「動算」となります。)
割り算の場合
割り算の場合、まず、( )個という分離数で等分に割って、その1つの断片を導き出す「等分除」があります。
さらに、6cmの縄を( )cmずつの連続量で分けるとき、何個に分けられるかを導き出す方法もあります。
(学習指導要領2020では、余りが出ない場合を「包含除」と表現している)
後者の場合、あまりが出る場合、答えに、( )個という分離数と( )cmという連続量が同時に出てきます。
数と量が混在しています。
6cm ÷4cm= 1個 余り 2cm
となりますね。
切り算・動算の場合
こうした不便や混乱を解消したのが、切り算・動算(どうざん)です。
分離数と連続量を同時に計算することができる上に、等分にするという命令がなく、自由に切り分けることができます。
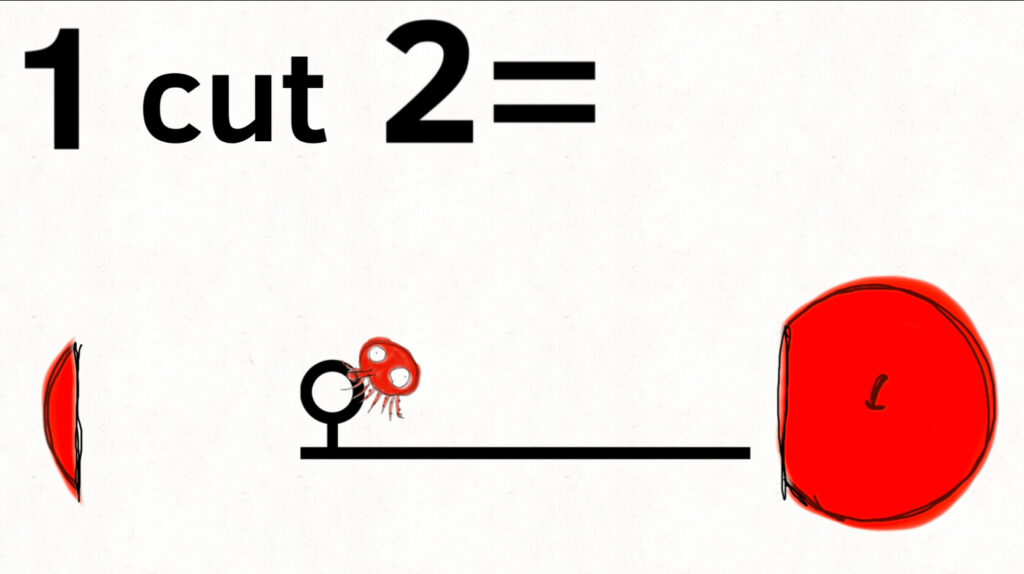
6cm cut 2=
これは、6cmの縄を2個に分けましょうという意味です。
この場合、
6cm cut 2個=
1cm+5cm
2cm+4cm
3cm+3cm
4cm+2cm
5cm+1cm
と、等分しなければならないという命令がなく、
さらに、0.001cm+5.999cmなど、自在に切り分けられ、2つの断片は残ります。
「+」の代わりに「오」というレバーを使うと、自由に切れ目が調整できます。
デジタルな数とアナログの量の両方を同時に計算することができ、現実をありのままに表現することができます。
概念が計算ができる動算の真価

さらに、通常の計算では、数字しか扱うことができません。
ところが、動算では、「概念」が計算できます。
元々、この研究は、人工自我(AE)にどうやったら道徳的な心、意識を持たせることができるか?というところから始まったものです。
ですから、人の意識についての洞察に基づいて、この新しい数式が発明されたのです。
左や右と認識するのも、人の脳内に「概念」があるからです。
人は、それぞれに、言葉や数学によってこの世界を「概念化」し、認識しています。
共通の概念の土台もありますが、人それぞれに、ちょっとずつズレています。
家庭環境や教育、社会、文化、宗教、時代的な背景によっても、ズレが生じます。
こうしたズレを多くの人は認識していませんし、自分の「概念」のクセも十分に理解できていません。
「概念化」は、人がこの世界を認識するために必要な道具ですが、このズレが様々な摩擦を生み出しています。
この数式の真価は、人工自我の進化だけでなく、人の意識への応用と拡張にあります。
つづく…
*文献:S. Mitsuyoshi, E. Shintani, K. Tomonaga, Y. Tei
WHITE HOLE EXISTENCE ON THE INVERSE UNIVERSE. Science & Philosophy, Vol. 10, No. 2, 2022.